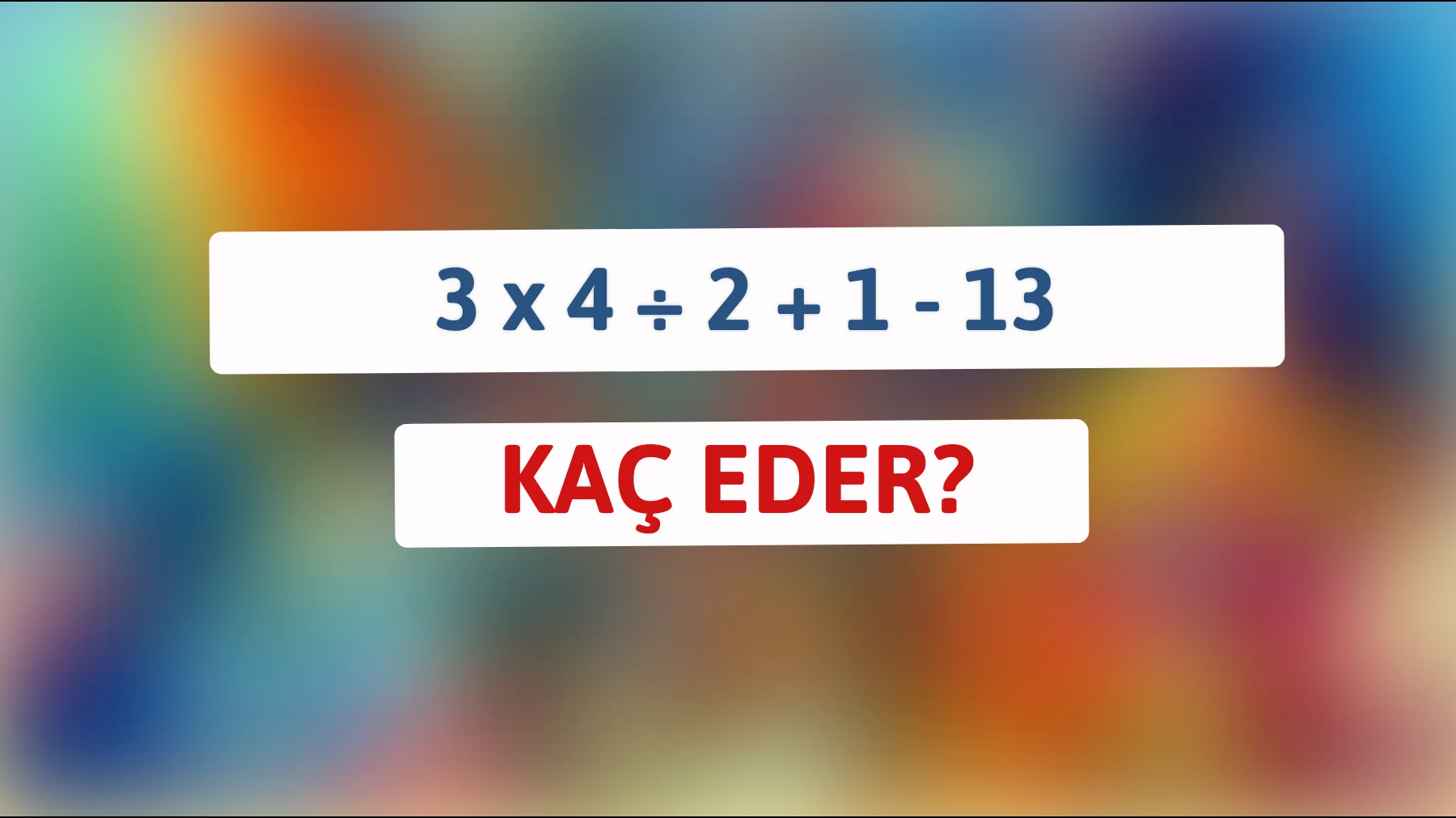Belki de sıradan bir hesaplama gibi görünse de, 3 x 4 ÷ 2 + 1 – 13 ifadesinin çözüme ulaştırılması, matematiğin inceliklerini ve ardındaki mantığı kavramak için harika bir fırsat sunuyor. Bu tür sorular, matematik problemleriyle uğraşmanın ne kadar zevkli ve düşündürücü olabileceğini gösterir.
Bu basit gibi görünen matematik problemi aslında zihnimizin matematiksel düşünme yeteneğini test ederken aynı zamanda aceleci davranmamanın önemini vurgular. Hemen hemen herkesin ilkokuldan beri karşılaştığı temel bir işlem olan sırayla işlem yapma kuralı, bu sorunun da temel taşıdır. Bu soruya bakarken, matematiksel işlem sırası kurallarını (öncelik sırası: çarpma ve bölme, ardından toplama ve çıkarma) yeniden gözden geçirme şansı buluyoruz.
İlk bakışta yanılgıya düşebilir ve belki de işlemleri soldan sağa yapma hatasına kapılabilirsiniz. Ancak burada asıl marifet **sadece doğru işlem sırasını uygulamak** değil, aynı zamanda zihinsel olarak doğru adımlar atarak sonuca ulaşmaktır. Şimdi gelin bu problemi birlikte ele alalım ve kendimizi bu zihinsel meydan okumaya hazırlayalım. Unutmayın, bu tür sorular matematiğe olan bakış açımızı zenginleştirir ve sayılarla olan ilişkimizi geliştirir.
Zihinsel Çeviklik ve Matematik
İşlemi adım adım çözmeye başladığımızda öncelikle çarpma ve bölme işlemlerini dikkate almalıyız. Burada sorumuz: **Kaç eder 3 x 4 ÷ 2 + 1 – 13?** Sorunuzun ilk kısmı çarpma ve bölmedir: 3 x 4 işlemi 12’yi verir, ardından 12 ÷ 2 işlemi ise 6 sonucunu doğurur. Bu öncelikli işlemler, matematikte genellikle “öncelik sırası” olarak bilinen temel bir kavramı hatırlatarak, zihin jimnastiği yapmamıza olanak tanır.
Ardından gelen toplama ve çıkarma işlemleriyle devam ettiğimizde ise daha az karmaşık görünen ama yine de dikkat gerektiren bir kısım bizleri bekliyor. Şimdi elimizde 6 var ve buna 1 ekliyoruz; sonuç 7 olur. Ama burada bitmiyor çünkü hemen ardından 13 çıkardığımızda, finale ulaşıyoruz: sonuç -6. Bu tür problemlerde attention to detail (detaylara dikkat) ve accuracy (doğruluk) kavramları büyük önem taşır.
Matematik ve Günlük Hayat: Negatif Sayılar
-6 sonucunu elde etmek belki de matematiksel bir zaferden daha fazlasıdır. Negatif sayılar, borçlar ya da sıcaklık değerleri gibi günlük hayatımızda farklı yerlerde karşımıza çıkabilecek kavramların anlaşılmasına olanak tanır. Aslında, negatif sayılar tarih boyunca matematiğe yapılan katkıların en önemlilerindendir. İlk kez Hint matematikçiler tarafından önerilen bu kavram, matematiğin nasıl evrim geçirdiğinin ve sürekli gelişiminin bir kanıtıdır. Negatif sayılar, karmaşık hesaplamalar ve denklemler için gerekli olan soyut bir düşünce yapısını temsil eder. Bu basit görünen problem, bu yüzden matematiğin hem zengin hem de heyecan verici dünyasına açılan bir kapı olabilir.
İşte böylece, 3 x 4 ÷ 2 + 1 – 13 sorusu aslında sadece bir işlem dizilimi değil; zihnimizi keskinleştirmenin, detaylara dikkat etmenin ve günlük yaşamımızın bir parçası olan soyut matematiksel kavramları kavramanın muazzam bir yolu. Böyle meydan okumalar beyninizin sınırlarını zorlar ve her bir tozunu silkeleyerek daha parlak düşünme becerileri kazandırır. Matematikte yol almak bazen sadece doğru yolda ilerlemekle değil, aynı zamanda her bir adımı sağlam atmakla da ilgilidir.